2nd Balkan Olympiad in Informatics
Thessaloniki, Greece, 1-6 October 1994

Day 1 - Problem 2 (40 points)



Computer networking requires that the computers in the network be linked. This problem considers a linear network in which the computers are chained together so that each one is connected to exactly two others except for the two computers on the ends of the chain which are connected to only one computer. In the picture shown below, the computers are the black dots and their locations in the network are identified by planar coordinates (relative to a coordinate system not shown in the picture).



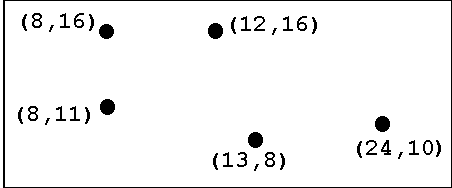
For various reasons it is desirable to minimize the length of the cable used. The problem is to determine how the computers should be connected in such a chain to minimize the total length of cable needed. In the installation being constructed, the cable will run beneath the floor, so that the amount of cable used to join 2 successive computers will be equal to the distance between the computers plus 10 additional meters of cable to connect from the floor to the computers and provide some slack for ease of installation.

Example :

  • Input:
    The input file will represent a data set beginning with a line consisting of a single number indicating the number of computers in the network (at least 2 and at most 10 computers). Then, in successive lines the coordinates are given as pairs of integer numbers (in the range [0..100]) separated by one or more space, e.g.
    5
    8 11
    8 16
    12 16
    13 8
    24 10

    The picture below shows the optimal way of connecting the computers shown above.



  • Output:
    The output should consist of n lines, where n is the number of computers. The first line should give the total length of cable needed. Subsequent lines should comprise of three numbers, l, s, e (from: length, start, end). The first number, l, should depict the length of the cable to be cut to connect the two computers, s and e. The values of s and e should represent the order of computers in the input. Any direction for traversing the network from the one end to the other is valid. For example,

    66.01
    14 3 2
    15 2 1
    15.83 1 4
    21.58 4 5