3rd Balkan Olympiad in Informatics
Varna, Bulgaria, 5-11 October 1995

Day 1 - Problem 1 (Reservoirs)



A system for fuel oil supply consists of n (n<=200) numbered reservoirs with given volumes (<=100) and n-1 tubes, assumed with zero volumes, that join pairs of reservoirs. The system is connected and it is filled up through one of the reservoirs s called source in the following manner. The sources s stay empty and pumps fuel oil so that per unit of time a unit of fuel goes through each of the tubes t1,t2, ...,tk joined to s, unit all reservoirs except the source are filled up. Therefore the process of filling takes time equal the maximum of V1,V2, ...,Vk, where Vi, for i=1,2,...,k is the sum of the volumes of the reservoirs that are filled up through tube ti.

Given the system of the described type, write a program that finds one optimal reservoir (source) from which the process of filling takes minimum time.

Input:
The program input will be given in an ASCII file name INPUT.1 with the following format:

line 1 : n is an integer denoting the number of the reservoirs
line i for i=2,...,n+1 : vi-1 is an integer denoting the volume of the reservoir i-1
line i for i=n+1,..,2n : r q is a pair of integers denoting that there is a tube between reservoir r and reservoir q. The numbers r,q are separated by one space.



Output:
The output should be one standard output (screen) and should contain two lines as follows:
The number of the optimal source is: ...
The optimal time is: ...

Example
The next figure shows an example with 11 reservoirs, that have equal unit volumes.


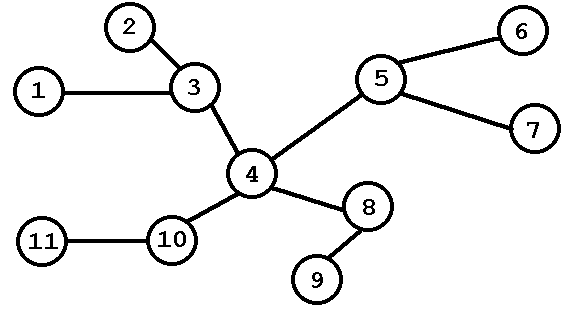
  • The input data for this example are:
    11
    1
    1
    1
    1
    1
    1
    1
    1
    1
    1
    11
    1 3
    2 3
    3 4
    4 5
    5 6
    5 7
    4 8
    8 9
    4 10
    10 11

  • The output should be:
    The number of the optimal source is: 4
    The optimal time is: 2